Christian D. Ott, Ernazar Abdikamalov, Philipp Moesta, Roland Haas, Steve Drasco, Evan O'Connor, Christian Reisswig, Casey Meakin, Erik Schnetter
ApJ 768, 115 (2013)
 |
Abstract
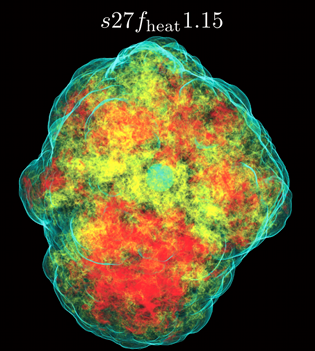
| We study the three-dimensional (3D) hydrodynamics of the post-core-bounce phase of the collapse of a 27 solar-mass star and pay special attention to the development of the standing accretion shock instability (SASI) and neutrino-driven convection. To this end, we perform 3D general-relativistic simulations with a 3-species neutrino leakage scheme with neutrino heating. Unlike "light-bulb" heating/cooling schemes, the leakage scheme captures the essential aspects of neutrino cooling, heating, and lepton number exchange as predicted by radiation-hydrodynamics simulations. The 27 solar-mass progenitor was studied in 2D by B. Mueller et al. (2012; arXiv:1205.7078), who observed strong growth of the SASI while neutrino-driven convection was suppressed. In our 3D simulations, neutrino-driven convection grows from numerical perturbations imposed by our Cartesian grid. It becomes the dominant instability and leads to large-scale non-oscillatory deformations of the shock front. These will result in strongly aspherical explosions without the need for large-scale SASI shock oscillations. Low-l-mode SASI oscillations are present in our models, but saturate at small amplitudes that decrease with increasing neutrino heating and vigor of convection. Our results suggest that once neutrino-driven convection is started, it is likely to become the dominant instability in 3D. Whether it is the primary instability after bounce will ultimately depend on the physical seed perturbations present in the cores of massive stars. The gravitational wave signal, which we extract and analyze for the first time from 3D general-relativistic models, will serve as an observational probe of the postbounce dynamics and, in combination with neutrinos, may allow us to determine the primary hydrodynamic instability. |
| See movie on YouTube. |
Gravitational Waveforms
We provide gravitational waveforms h+ and hx for equatorial and polar observers (in the source frame). The waveforms are rescaled by distance D and have units of cm. We also provide the six components Hlm from which the quadrupole waveforms seen from any angle can be constructed (see Ajith et al. 2007, arXiv:0709.0093. See the paper for details on extraction methods and discussions of the four models, which differ only by the degree of neutrino heating and by the perturbations imposed by the computational grid. Please contact Christian Ott (cott # tapir.caltech.edu) should you have any questions.
| Model Name | h+D and hxD at pole and equator | Hlm D |
| s27fheat1.00 | download | download |
| s27fheat1.05 | download | download |
| s27fheat1.10 | download | download |
| s27fheat1.15 | download | download |
| Download everything (13 MB) |
Simulation Source Code
The simulations were carried out with the Zelmani core collapse simulation package, which is based on the Einstein Toolkit, which, in turn, uses the Cactus Computational Toolkit and the Carpet adaptive mesh refinement driver. While not all components of Zelmani are open source yet, we can already provide as open source the leakage/heating module used in this study, ZelmaniLeak. ZelmaniLeak is a Cactus Thorn and should build smoothly in any regular Einstein Toolkit build. It requires other publically the Einstein Toolkit modules and the module CoreCollapseControl, which we provide as well.
Please contact Christian Ott (cott # tapir.caltech.edu) should you have any questions.
| Download CoreCollapseControl20121025.tar_.gz |
| Download ZelmaniLeak20121025.tar.gz |
The parameters used for the electron fraction parameterization used in the collapse phase are as follows:
# ye of rho parameters ZelmaniLeak::yeofrho_rho1 = 1.0e7 ZelmaniLeak::yeofrho_rho2 = 1.0e13 ZelmaniLeak::yeofrho_ye1 = 0.5e0 ZelmaniLeak::yeofrho_ye2 = 0.29e0 ZelmaniLeak::yeofrho_yec = 0.035e0 ZelmaniLeak::yeofrho_do_high_correction = yes ZelmaniLeak::yeofrho_high_correction_ye = 0.2717e0 ZelmaniLeak::yeofrho_high_correction_rho = 2.55e14