Christian D. Ott, Adam Burrows, Eli Livne, Rolf Walder
Astrophysical Journal, 600, 834 (2004).
- Gravitational Wave Signature Data -
Abstract
| We have carried out an extensive set of two-dimensional, axisymmetric, purely-hydrodynamic calculations of rotational stellar core collapse with a realistic, finite-temperature nuclear equation of state and realistic massive star progenitor models. For each of the total number of 72 different simulations we performed, the gravitational wave signature was extracted via the quadrupole formula in the slow-motion, weak-field approximation. We investigate the consequences of variation in the initial ratio of rotational kinetic energy to gravitational potential energy and in the initial degree of differential rotation. Furthermore, we include in our model suite progenitors from recent evolutionary calculations that take into account the effects of rotation and magnetic torques. For each model, we calculate gravitational radiation wave forms, characteristic wave strain spectra, energy spectra, final rotational profiles, and total radiated energy. In addition, we compare our model signals with the anticipated sensitivities of the 1st- and 2nd-generation LIGO detectors coming on line. We find that most of our models are detectable by LIGO from anywhere in the Milky Way. |
| Please note that the results of this study were obtained with calculations that did not incorporate general relativistic effects and deleptonization (via electron capture on protons) during collapse. Recent results by Ott et al. (2007), Dimmelmeier et al. (2007), and Dimmelmeier et al. 2008 suggest that deleptonization and general relativity have a significant quantitative and qualitative effect on the gravitational wave signature of rotating core collapse. Below we provide the gravitational wave signature data of all our models. The files are named according to the following nomenclature: |
||
[initial model name]A[value of A in km]B[value of initial beta=T/|W| in percent] |
||
Where beta is the initial ratio of rotational kinetic to gravitational potential energy and A controls the degree of differential rotation in the rotation law |
||
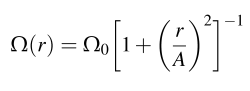 |
||
| in which r is the distance from the rotation axis. For example, setting A to 500 km leads to approximately solid body rotation within 500 km of the rotation axis. For more details please see the discussion in our paper. | ||
| We provide two types of data files. Files ending with .trh contain time (in seconds), maximum density (in g/cm^3), and dimensionless gravitational wave strain data (scaled to 10 kpc distance). The files ending with .spect contain the gravitational wave energy spectra in units M_sun c^2 / Hz. | ||
| 11 solar mass initial model (s11 from Woosley & Weaver 1995, ApJS 101, 181) | Summary Table | Complete set of model data files: s11complete.tar.gz |
| 15 solar mass initial model (s15 from Woosley & Weaver 1995, ApJS 101, 181 ) | Summary Table | Complete set of model data files: s15complete.tar.gz |
| 20/25 solar mass initial model (s20 from Woosley & Weaver 1995, ApJS 101, 181) | Summary Table | Complete set of model data files: s20complete.tar.gz |
| Models from Heger 2000, ApJ 528, 368 and Heger et al. 2003, Stellar Rotation, Proceedings IAU Symposium No. 215 |
Summary Table | Complete set of model data files: hegercomplete.tar.gz |